Algorithm performance time is related to input size
Time Complexity; consider very big input size N
So, not meaningful for coefficient or constant
It's just depend on N (input size)
- O(g(x)) means always f(x) <= K * g(x)
- There are too many options for Big O
- So, select the smallest range of Big O (meaningful)
(cf. if log function; just ignore base => use base e (Euler's constant)
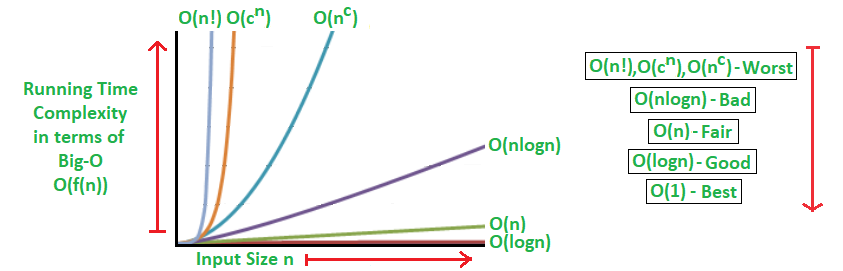
so, use log or ln) - Performance time standard: O(logn) >> O(n); O(logn) is more scalable(extensible)
- Worst case
- f(x) >= k * g(n)
- At the earliest f, f is slower than g.
- Best case
- It can be Big Omega and Big O
- Both bounding
- Average case
(Algorithm evaluation standard)
- O(1): constant (time complexity)
- O(logn): logarithmic
- O(n): linear
- O(n^2): quadratic
(cf. O(n^k) for k >= 1: Polynomial) - O(n^3): cubic
- O(2^n), O(k^n), O(n!): exponential
-
? => Big O? Big Omega? Big Theta?
-
The answer is Big O
- Big O's definition: abs(f(x)) <= C * abs(g(x)) for all x >= k (C, k > 0, constant)
Prove: abs(4n^2 + 2n - 1) <= C * abs(n^2), for all n >= k
let, k = 1, C = 6
=> abs(4n^2 + 2n - 1) <= 6 * abs(n^2), for all n >= 1
=> 4n^2 + 2n - 1 <= 6 * n^2, for all n >= 1
(because 4n^2 + 2n - 1 and n^2 are increase function when n >= 1)
<Use Inequality method>
=> 4n^2 + 2n - 1 < 4n^2 + 2n <= 4n^2 + 2n^2
=> 4n^2 + 2n - 1 < 4n^2 + 2n <= 6n^2
=> 4n^2 + 2n - 1 < 6n^2
so, f(n) = O(n^2)
* Tip) We just prove C, k (constant, greater than 0, real number) exist on that inequality
* Big Theta; prove Big O and Big Omega both cases
Prove: abs(n + 30) <= C * abs(n^3), for all n >= k, [C, k exists]
let, C = 31, k = 2
=> abs(n + 30) <= 31 * abs(n^3), for all n >= 2
=> n + 30 <= 31 * n^3, for all n >= 2
(because n + 30 and n^3 are positive number when n >= 2)
=> n + 30 <= 31 * n^3
<Use Division method>
=> ((n + 30) / (31 * n^3)) <= 1
=> (1 / (31 * n^2) + 30 / (31 * n^3)) <= 1
=> (1 / (31 * n^2) + 30 / (31 * n^3)) <= (1 / 31) * (1 / 2^2) + (30 / 31) * (1/ 2^3) <= 1
(because 1 / (31 * n^2) and 30 / (31 * n^3) are decrease function when n >= 2)
so, f(n) = O(n^3)
cf). <Use Inequality method>
n + 30 <= 31 * n^3
=> n + 30 < n^2 * (n + 30) < n^3 + 30 * n^2 * n (= 31 * n^3)
=> n + 30 <= 31 * n^3
<Use Graph method>
let C = 100, k = 32
=> (left term) log2 32 = 5
(right term) 100 * 32 = 3200
=> 5 <= 3200 (that difference is getting bigger as check two function graph)
So, f(n) = O(n)