Soft_Computing_Techniques

Soft Computing Techniques

M. Sc (Information Technology) PSIT1P4 Soft Computing Techniques

Index

Sr.No.	Name	ReadME
Prac1A-i Prac1A-ii	1A-i. Design a simple linear neural network model. 1A-ii. Calculate the output of neural net for given data.	Prac1A-i Prac1A-ii
Prac1B	1B. Calculate the output of neural net using both binary and bipolar sigmoidal function.	Prac1B
Prac2A	2A. Generate AND/NOT function using McCulloch- Pitts neural net.	Prac2A
Prac2B	2B. Generate XOR function using McCulloch-Pitts neural net.	Prac2B
Prac3A	3A. Write a program to implement Hebb’s rule.	Prac3A
Prac3B	3B. Write a program to implement of delta rule.	Prac3B
Prac4A	4A. Write a program for Back Propagation Algorithm.	Prac4A
Prac4B	4B. Write a program for error Backpropagation algorithm.	Prac4B
Prac5A	5A. Write a program for hopfield network.	Prac5A
Prac5B	5B. Write a program for radial basis function.	Prac5B
Prac6A	6A. Kohonen self organizing map.	Prac6A
Prac6B	6B. Hopfield network.	Prac6B
Prac7A-i Prac7A-ii	7A-i. Implement membership and identity operators - in 7A-ii. Implement membership and identity operators- not in.	Prac7A-i Prac7A-ii
Prac7B-i Prac7B-ii	7B-i. Implement membership and identity operators- is. 7B-ii. Implement membership and identity operators- is not.	Prac7B-i Prac7B-ii
Prac8A	8A. Find ratios using fuzzy logic.	Prac8A
Prac8B	8B. Solve tipping problem using fuzzy logic.	Prac8B

---

---

Prac1A-i

• 1A-i. Design a simple linear neural network model.

x = float(input("\n Enter the input x = "))
w = float(input("\n Enter the weight w = "))
b = float(input("\n Enter the bias b  = "))

yin = w * x + b
print("\n Next input yin ", yin)

print("\n ************OUTPUT**************")
if yin < 0:
    output = 0
elif yin > 1:
    output = 1
else:
    output = yin

print("Output", output)

• OUTPUT

---

Prac1A-ii

• 1A-ii. Calculate the output of neural net for given data.

# 1A-ii. Calculate the output of neural net for given data.
n = int(input("Enter the number of input: "))
yin = 0

for i in range(n):
    x = float(input("Enter x :"))
    w = float(input("Enter weight w: "))
    yin = yin + x * w

print("Output ", yin)

if yin < 0:
    output = 0
elif yin > 1:
    output = 1
else:
    output = yin

print("Output: ", output)

• OUTPUT

---

Prac1B

• 1B. Calculate the output of neural net using both binary and bipolar sigmoidal function.

# 1B. Calculate the output of neural net using both binary and bipolar sigmoidal function.
import math
n = int(input("Enter the number of element "))
yin = 0
for i in range(0, n):
    x = float(input("Enter x :"))
    w = float(input("Enter weight w: "))
    yin = yin + x * w

b = float(input("B "))
yin = yin + b
print("yin ", yin)

binary_sigmoidal = 1 / (1 + (math.e ** (-yin)))
print("Binary Sigmoidal = ", round(binary_sigmoidal, 3))

bipolar_sigmoidal = (2 / (1 + (math.e ** (-yin)))) - 1
print("Bipolar Sigmoidal = ", round(bipolar_sigmoidal, 3))

• OUTPUT

---

Prac2A

• 2A. Generate AND/NOT function using McCulloch- Pitts neural net.

# 2A. Generate AND/NOT function using McCulloch- Pitts neural net.

print("ANDNOT function using McCulloch-pitts\n")
x1inputs = [1, 1, 0, 0]
x2inputs = [1, 0, 1, 0]

print("Considering one weight as excitatory and other as inhibitory")
w1 = [1, 1, 1, 1]
w2 = [-1, -1, -1, -1]

yin = []
print("x1", "x2", "yin")
for i in range(0, 4):
    yin.append(x1inputs[i] * w1[i] + x2inputs[i] * w2[i])
    print(x1inputs[i], "   ", x2inputs[i], "  ", yin[i])

theta = 2 * 1 - 1  # n *w -p
print("Threshold-theta - ", theta)
print("Applying Threshold - ", theta)
Y = []
for i in range(0, 4):
    if yin[i] >= theta:
        value = 1
        Y.append(value)
    else:
        value = 0
        Y.append(value)
print("x1 ", "x2", "Y")
for i in range(0, 4):
    print(x1inputs[i], " ", x2inputs[i], " ", Y[i])

• OUTPUT

---

Prac2B

• 2B. Generate XOR function using McCulloch-Pitts neural net.

# 2B. Generate XOR function using McCulloch-Pitts neural net.

print("XOR function using McCulloch-pitts\n")
x1inputs = [1, 1, 0, 0]
x2inputs = [1, 0, 1, 0]

print("Calculating z1 = x1w11 + x2w21")
print("Considering one weights as excitatory and other as inhibitory")
w11 = [1, 1, 1, 1]
w21 = [-1, -1, -1, -1]

print("x1", "x2", "z1")
z1 = []
for i in range(0, 4):
    z1.append(x1inputs[i] * w11[i] + x2inputs[i] * w21[i])
    print(x1inputs[i], "   ", x2inputs[i], "  ", z1[i])

# Z2
print("Calculating z2 = x1w12 + x2w22")
print("Considering one weights as inhibitory and other as excitatory")
w12 = [-1, -1, -1, -1]
w22 = [1, 1, 1, 1]

print("x1", "x2", "z2")
z2 = []
for i in range(0, 4):
    z2.append(x1inputs[i] * w12[i] + x2inputs[i] * w22[i])
    print(x1inputs[i], "   ", x2inputs[i], "  ", z2[i])

print("Applying threshold for x1 and x2")
for i in range(0, 4):
    if z1[i] >= 1:
        z1[i] = 1
    else:
        z1[i] = 0
    if z2[i] >= 1:
        z2[i] = 1
    else:
        z2[i] = 0
print("z1", "z2")
for i in range(0, 4):
    print(z1[i], " ", z2[i])

print("x1 ", "x2", "Yin")
yin = []
v1 = 1
v2 = 1
for i in range(0, 4):
    yin.append(z1[i] * v1 + z2[i] * v2)
    print(x1inputs[i], " ", x2inputs[i], " ", yin[i])

print("Applying Threshold=1 for yin")
print("x1", "x2", "yin")
y = []
for i in range(0, 4):
    if yin[i] >= 1:
        y.append(1)
    else:
        y.append(0)
for i in range(0, 4):
    print(x1inputs[i], " ", x2inputs[i], " ", y[i])

print("END")

• OUTPUT

---

Prac3A

• 3A. Write a program to implement Hebb’s rule.

# 3A. Write a program to implement Hebb’s rule.

import numpy as np

x1 = np.array([1, -1, -1, 1, -1, -1, 1, 1, 1])
x2 = np.array([1, -1, 1, 1, -1, 1, 1, 1, 1])
b = 0

y = np.array([1, -1])
wtold = np.zeros((9,))
wtnew = np.zeros((9,))

wtnew = wtnew.astype(int)
wtold = wtold.astype(int)

bais = 0
print("First input with target = 1")
for i in range(0, 9):
    wtnew[i] = wtold[i] + x1[i] * y[0]
wtold = wtnew
b = b + y[0]
print("New wt=", wtnew)
print("Bias value ", b)
print("**********************************")
print("second input with target = 1")
for i in range(0, 9):
    wtnew[i] = wtold[i] + x2[i] * y[1]
wtold = wtnew
b = b + y[1]
print("New wt=", wtnew)
print("Bias value= ", b)

• OUTPUT

---

Prac3B

• 3B. Write a program to implement of delta rule.

# 3B. Write a program to implement of delta rule.

print("b) Aim: - Write a program to implement delta rule")
import numpy as np
import time

np.set_printoptions(precision=2)
x = np.zeros((3,))
weights = np.zeros((3,))
desired = np.zeros((3,))
actual = np.zeros((3,))
for i in range(0, 3):
    x[i] = float(input("Intial inputs: "))
for i in range(0, 3):
    weights[i] = float(input("Intial weights: "))
for i in range(0, 3):
    desired[i] = float(input("Desired output: "))
a = float(input("Enter learning rate: "))
actual = x * weights
print("Acrual ", actual)
print("Desired ", desired)
while True:
    if np.array_equal(desired, actual):
        break
    else:
        for i in range(0, 3):
            weights[i] = weights[i] + a * (desired[i] - actual[i])
            actual = x * weights
print("Weights ", weights)
print("Actual ", actual)
print("Desired ", desired)
print("*" * 30)
print("Final output")
print("Corrected weights", weights)
print("Actual", actual)
print("Desired ", desired)

• OUTPUT

---

Prac4A

• 4A. Write a program for Back Propagation Algorithm.

# 4A. Write a program for Back Propagation Algorithm.

import numpy as np

X = np.array(([2, 9], [1, 5], [3, 6]), dtype=float)
Y = np.array(([92], [86], [89]), dtype=float)
X = X / np.amax(X, axis=0)
Y = Y / 100

class NN(object):
    def __init__(self):
        self.inputsize = 2
        self.outputsize = 1
        self.hiddensize = 3
        self.W1 = np.random.randn(self.inputsize, self.hiddensize)
        self.W2 = np.random.randn(self.hiddensize, self.outputsize)

    def forward(self, X):
        self.z = np.dot(X, self.W1)
        self.z2 = self.sigmoidal(self.z)
        self.z3 = np.dot(self.z2, self.W2)
        op = self.sigmoidal(self.z3)
        return op

    def sigmoidal(self, s):
        return 1 / (1 + np.exp(-s))

obj = NN()
op = obj.forward(X)
print("actual output\n" + str(op))
print("expected output\n" + str(Y))

• OUTPUT

---

Prac4B

• 4B. Write a program for error Backpropagation algorithm.

# 4B. Write a program for error Backpropagation algorithm.

import numpy as np

X = np.array(([2, 9], [1, 5], [3, 6]), dtype=float)
Y = np.array(([92], [86], [89]), dtype=float)

X = X / np.amax(X, axis=0)
Y = Y / 100

class NN(object):
    def __init__(self):
        self.inputsize = 2
        self.outputsize = 1
        self.hiddensize = 3
        self.W1 = np.random.randn(self.inputsize, self.hiddensize)
        self.W2 = np.random.randn(self.hiddensize, self.outputsize)

    def forward(self, X):
        self.z = np.dot(X, self.W1)
        self.z2 = self.sigmoidal(self.z)
        self.z3 = np.dot(self.z2, self.W2)
        op = self.sigmoidal(self.z3)
        return op

    def sigmoidal(self, s):
        return 1 / (1 + np.exp(-s))

    def sigmoidalprime(self, s):
        return s * (1 - s)

    def backward(self, X, Y, o):
        self.o_error = Y - o
        self.o_delta = self.o_error * self.sigmoidalprime(o)
        self.z2_error = self.o_delta.dot(self.W2.T)
        self.z2_delta = self.z2_error * self.sigmoidalprime(self.z2)
        self.W1 = self.W1 + X.T.dot(self.z2_delta)
        self.W2 = self.W2 + self.z2.T.dot(self.o_delta)

    def train(self, X, Y):
        o = self.forward(X)
        self.backward(X, Y, o)

obj = NN()
for i in range(2000):
    print("input\n" + str(X))
    print("Actual output\n" + str(Y))
    print("Predicted output\n" + str(obj.forward(X)))
    print("loss\n" + str(np.mean(np.square(Y - obj.forward(X)))))
    obj.train(X, Y)

• OUTPUT

---

Prac5A

• 5A. Write a program for hopfield network.

# 5A. Write a program for hopfield network.

import numpy as np

def compute_next_state(state, weight):
    # @ is a shorthand for 'np.matmul()'
    # the numpy.where() function return thr indices of
    # element in an input array where condition is satisfied
    next_state = np.where(weight @ state >= 0, +1, -1)
    return next_state

def compute_final_state(initial_state, weight, max_iter=1000):
    previous_state = initial_state
    next_state = compute_next_state(previous_state, weight)
    is_stable = np.all(previous_state == next_state)
    n_iter = 0
    while (not is_stable) and (n_iter <= max_iter):
        previous_state = next_state
        next_state = compute_next_state(previous_state, weight)
        print("Previous State: ", previous_state)
        print("Next State: ", next_state)
        is_stable = np.all(previous_state == next_state)
        n_iter += 1
    return previous_state, is_stable, n_iter

initial_state = np.array([+1, -1, -1, -1])
weight = np.array([[0, -1, -1, +1], [-1, 0, +1, -1], [-1, +1, 0, -1], [+1, -1, -1, 0]])
final_state, is_stable, n_iter = compute_final_state(initial_state, weight)
print("final State : ", final_state)
print("is_stable : ", is_stable)

• OUTPUT

---

Prac5B

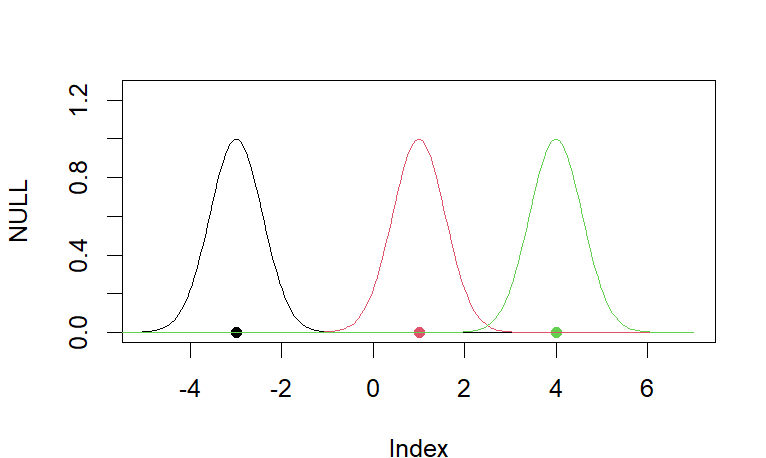
• 5B. Write a program for radial basis function(R language).

# 5B. Write a program for radial basis function.
# R language
D <- matrix(c(-3, 1, 4), ncol = 1) # 3 datapoints
N <- length(D)
rbf.gauss <- function(gamma = 1.0) {
    function(x) {
        exp(-gamma * norm(as.matrix(x), "F")^2)
    }
}
xlim <- c(-5, 7)
print(N)
print(xlim)
plot(NULL, xlim = xlim, ylim = c(0, 1.25), type = "n")
points(D, rep(0, length(D)), col = 1:N, pch = 19)
x.coord <- seq(-7, 7, length = 250)
gamma <- 1.5
for (i in 1:N) {
    points(x.coord, lapply(x.coord - D[i, ], rbf.gauss(gamma)), type = "l", col = i)
}

• OUTPUT

---

Prac6A

• 6A. Kohonen self organizing map

# 6A. Kohonen self organizing map.
from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt

colors = [
    [0.0, 0.0, 0.0],
    [0.0, 0.0, 1.0],
    [0.0, 0.0, 0.5],
    [0.125, 0.529, 1.0],
    [0.33, 0.4, 0.67],
    [0.6, 0.5, 1.0],
    [0.0, 1.0, 0.0],
    [1.0, 0.0, 0.0],
    [0.0, 1.0, 1.0],
    [1.0, 0.0, 1.0],
    [1.0, 1.0, 0.0],
    [1.0, 1.0, 1.0],
    [0.33, 0.33, 0.33],
    [0.5, 0.5, 0.5],
    [0.66, 0.66, 0.66],
]

color_names = [
    "black",
    "blue",
    "darkblue",
    "skyblue",
    "greyblue",
    "lilac",
    "green",
    "red",
    "cyan",
    "violet",
    "yellow",
    "white",
    "darkgrey",
    "mediumgrey",
    "lightgrey",
]

som = MiniSom(30, 30, 3, sigma=3.0, learning_rate=2.5, neighborhood_function="gaussian")

plt.imshow(abs(som.get_weights()), interpolation="none")
som = MiniSom(30, 30, 3, sigma=8.0, learning_rate=0.5, neighborhood_function="bubble")

som.train_random(colors, 500, verbose=True)
plt.imshow(abs(som.get_weights()), interpolation="none")

• OUTPUT

---

Prac6B

• 6B. Hopfield network.

# 6B. Hopfield network.

from neurodynex.hopfield_network import network, pattern_tools, plot_tools
import matplotlib.pyplot as plt

pattern_size = 5
# create an instance of the class HopfieldNetwork
hopfield_net = network.HopfieldNetwork(nr_neurons=pattern_size ** 2)
# instantiate a pattern factory
factory = pattern_tools.PatternFactory(pattern_size, pattern_size)

# create a checkerboard pattern and add it to the pattern list
checkerboard = factory.create_checkerboard()
pattern_list = [checkerboard]

# add random patterns to the list
pattern_list.extend(
    factory.create_random_pattern_list(nr_patterns=3, on_probability=0.5)
)
plot_tools.plot_pattern_list(pattern_list)

# how similar are the random patterns and the checkerboard? Check the overlaps
overlap_matrix = pattern_tools.compute_overlap_matrix(pattern_list)
plot_tools.plot_overlap_matrix(overlap_matrix)

# let the hopfield network "learn" the patterns. Note: they are not stored
# explicitly but only network weights are updated !
hopfield_net.store_patterns(pattern_list)

# create a noisy version of a pattern and use that to initialize the network
noisy_init_state = pattern_tools.flip_n(checkerboard, nr_of_flips=4)
hopfield_net.set_state_from_pattern(noisy_init_state)

# from this initial state, let the network dynamics evolve.
states = hopfield_net.run_with_monitoring(nr_steps=4)

# each network state is a vector. reshape it to the same shape used to create the patterns.
states_as_patterns = factory.reshape_patterns(states)

# plot the states of the network
plot_tools.plot_state_sequence_and_overlap(
    states_as_patterns, pattern_list, reference_idx=0, suptitle="Network dynamics"
)

• OUTPUT

---

Prac7A-i

• 7A-i. Implement membership and identity operators in

# 7A-i. Implement membership and identity operators *in*.

list1 = []
print("Enter 5 numbers")
for i in range(0, 5):
    v = int(input())
    list1.append(v)
list2 = []
print("Enter 5 numbers")
for i in range(0, 5):
    v = int(input())
    list2.append(v)
flag = 0
for i in list1:
    if i in list2:
        flag = 1
if flag == 1:
    print("The Lists Overlap")
else:
    print("The Lists do Not overlap")

• OUTPUT

---

Prac7A-ii

• 7A-ii. Implement membership and identity operators not in

# 7A-ii. Implement membership and identity operators *not in*.

list1 = []
c = int(input("Enter the number of elements that you want to insert in List 1:"))
for i in range(0, c):
    ele = int(input("Enter the element :"))
    list1.append(ele)
a = int(input("enter the number that you want to find in List 1:"))
if a not in list1:
    print("The list does not contain ", a)
else:
    print("The list contains", a)

• OUTPUT

---

Prac7B-i

• 7B-i. Implement membership and identity operators is.

# 7B-i. Implement membership and identity operators *is*.

details = []
name = input("Enter your name : ")
details.append(name)
age = float(input("Enter your exact age : "))
details.append(age)
roll_no = int(input("Enter your roll no : "))
details.append(roll_no)
for i in details:
    print(i)
    print("Int = ", type(i) is int)
    print("Float = ", type(i) is float)
    print("String = ", type(i) is str)
    print()

• OUTPUT

---

Prac7B-ii

• 7B-ii. Implement membership and identity operators is not.

# 7B-ii. Implement membership and identity operators *is not*.

details = []
name = input("Enter your name : ")
details.append(name)
age = float(input("Enter your exact age : "))
details.append(age)
roll_no = int(input("Enter your roll no : "))
details.append(roll_no)
print()
for i in details:
    print(i)
    print("Not Int = ", type(i) is not int)
    print("Not Float = ", type(i) is not float)
    print("Not String = ", type(i) is not str)
    print()

• OUTPUT

---

Prac8A

• 8A. Find ratios using fuzzy logic.

# 8A. Find ratios using fuzzy logic.

from fuzzywuzzy import fuzz
from fuzzywuzzy import process

s1 = "My name is ABC"
s2 = "I am ABC"
print("FuzzyWuzzy Ratio:", fuzz.ratio(s1, s2))
print("FuzzyWuzzy PartialRatio: ", fuzz.partial_ratio(s1, s2))
print("FuzzyWuzzy TokenSortRatio: ", fuzz.token_sort_ratio(s1, s2))
print("FuzzyWuzzy TokenSetRatio: ", fuzz.token_set_ratio(s1, s2))
print("FuzzyWuzzy WRatio: ", fuzz.WRatio(s1, s2), "\n\n")

# for process library,
query = "fuzzys for fuzzys"
choices = ["fuzzy for fuzzy", "fuzzy fuzzy", "g. for fuzzys"]
print("List of ratios: ")
print(process.extract(query, choices), "\n")
print("Best among the above list: ", process.extractOne(query, choices))

• OUTPUT

---

Prac8B

• 8B. Solve tipping problem using fuzzy logic.

# 8B. Solve tipping problem using fuzzy logic.
# google.colab
!pip install fuzzywuzzy
!pip install -U scikit-fuzzy

import skfuzzy as fuzz
from skfuzzy import control as ctrl
import numpy as np
quality = ctrl.Antecedent(np.arange(0, 11, 1), 'quality')
service = ctrl.Antecedent(np.arange(0, 11, 1), 'service')
tip = ctrl.Consequent(np.arange(0, 26, 1), 'tip')

quality.automf(3)
service.automf(3)

tip['low'] = fuzz.trimf(tip.universe, [0, 0, 13])
tip['medium'] = fuzz.trimf(tip.universe, [0, 13, 25])
tip['high'] = fuzz.trimf(tip.universe, [13, 25, 25])

quality['average'].view()
service.view()
tip.view()

rule1 = ctrl.Rule(quality['poor'] | service['poor'], tip['low'])
rule2 = ctrl.Rule(service['average'], tip['medium'])
rule3 = ctrl.Rule(service['good'] | quality['good'], tip['high'])

rule1.view()

tipping_ctrl = ctrl.ControlSystem([rule1, rule2, rule3])
tipping = ctrl.ControlSystemSimulation(tipping_ctrl)

tipping.input['quality'] = 6.5
tipping.input['service'] = 9.8

tipping.compute()
print (tipping.output['tip'])
tip.view(sim=tipping)

• OUTPUT

---

Go To Top