Skip to content

Latest commit

 

History

History
139 lines (93 loc) · 5.39 KB

3-3-平衡查找树.md

File metadata and controls

139 lines (93 loc) · 5.39 KB

平衡查找树

前几种算法在最坏情况下的性能还是很糟糕。本节中介绍一种二分查找树并能保证无论如何构造它，它的运行时间都是对数级别的。

理想情况下，我们希望能够保持二分查找树的平衡性，以使树高为 ~lgN，这样就能保证所有查找都能在 ~lgN 次比较内结束。

3.3.1 2-3查找树

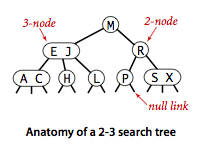
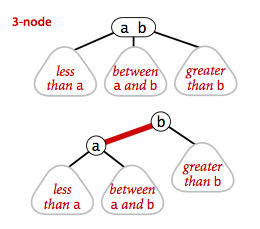
为了保持平衡性，2-3 查找树引入了 2- 节点和 3- 节点，目的是为了让树平衡。一颗完美平衡的 2-3 查找树的所有空链接到根节点的距离应该是相同的。

3.3.1.1 查找

3.3.1.2 插入

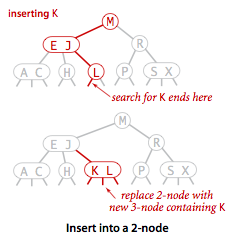
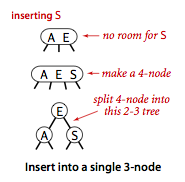
插入操作和 BST 的插入操作有很大区别，BST 的插入操作是先进行一次未命中的查找，然后再将节点插入到对应的空链接上。但是 2-3 查找树如果也这么做的话，那么就会破坏了平衡性。它是将新节点插入到叶子节点上。

根据叶子节点的类型不同，有不同的处理方式：

  • 如果插入到 2- 节点上，那么直接将新节点和原来的节点组成 3- 节点即可。

  • 如果是插入到 3- 节点上，就会产生一个临时 4- 节点时，需要将 4- 节点分裂成 3 个 2- 节点，并将中间的 2- 节点移到上层节点中。如果上移操作继续产生临时 4- 节点则一直进行分裂上移，直到不存在临时 4- 节点。

3.3.1.3性质

2-3 查找树插入操作的变换都是局部的，除了相关的节点和链接之外不必修改或者检查树的其它部分，而这些局部变换不会影响树的全局有序性和平衡性。

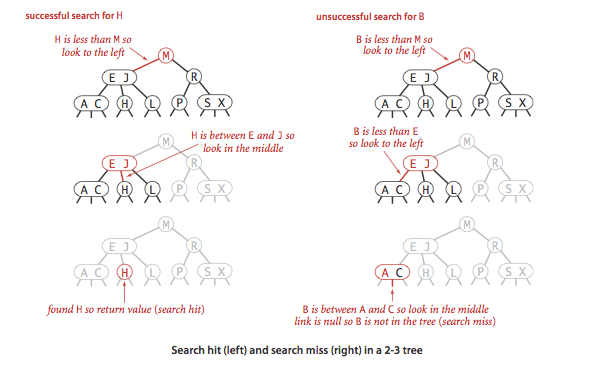
2-3 查找树的查找和插入操作复杂度和插入顺序无关，在最坏的情况下查找和插入操作访问的节点必然不超过 logN 个，含有 10 亿个节点的 2-3 查找树最多只需要访问 30 个节点就能进行任意的查找和插入操作。

3.3.2 红黑二叉查找树

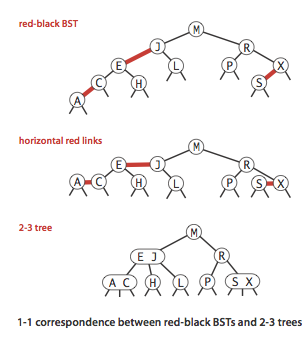
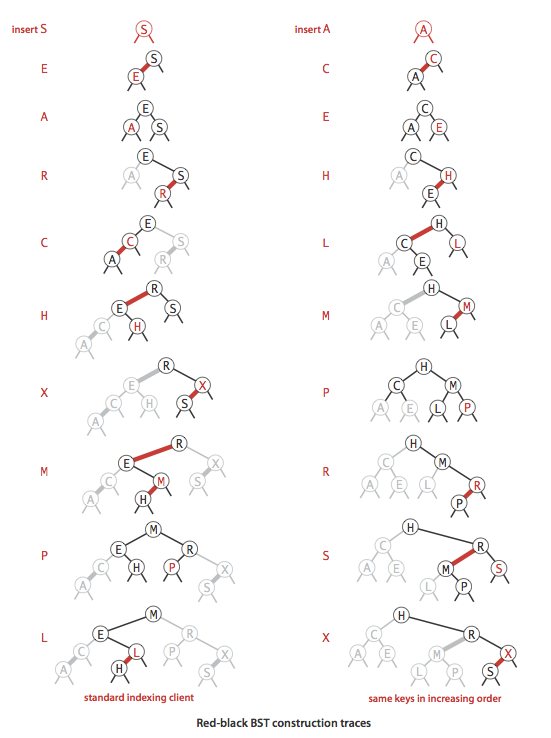
红黑树是 2-3 查找树，但它不需要分别定义 2- 节点和 3- 节点，而是在普通的二叉查找树之上，为节点添加颜色。指向一个节点的链接颜色如果为红色，那么这个节点和上层节点表示的是一个 3- 节点，而黑色则是普通链接。

红黑树具有以下性质：

  • 红链接都为左链接；
  • 完美黑色平衡，即任意空链接到根节点的路径上的黑链接数量相同。

画红黑树时可以将红链接画平。

public class RedBlackBST<Key extends Comparable<Key>, Value> extends BST<Key, Value> {

    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private boolean isRed(Node x) {
        if (x == null)
            return false;
        return x.color == RED;
    }
}

3.3.2.1 左旋转

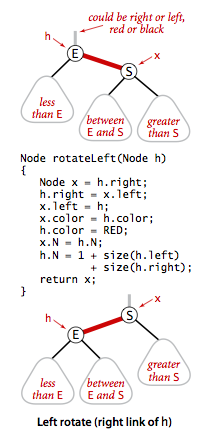
因为合法的红链接都为左链接，如果出现右链接为红链接，那么就需要进行左旋转操作。

public Node rotateRight(Node h) {
    Node x = h.left;
    h.left = x.right;
    x.color = h.color;
    h.color = RED;
    x.N = h.N;
    recalculateSize(h);
    return x;
}

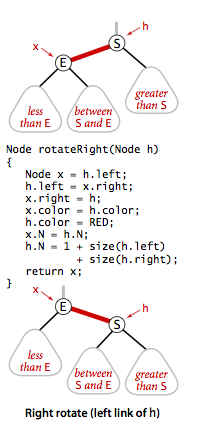
右旋转同理：

3.3.3 插入

先将一个节点按二叉查找树的方法插入到正确位置，然后再进行如下颜色操作：

  • 如果右子节点是红色的而左子节点是黑色的，进行左旋转；
  • 如果左子节点是红色的，而且左子节点的左子节点也是红色的，进行右旋转；
  • 如果左右子节点均为红色的，进行颜色转换。
@Override
public void put(Key key, Value value) {
    root = put(root, key, value);
    root.color = BLACK;
}

private Node put(Node x, Key key, Value value) {
    if (x == null) {
        Node node = new Node(key, value, 1);
        node.color = RED;
        return node;
    }
    int cmp = key.compareTo(x.key);
    if (cmp == 0)
        x.val = value;
    else if (cmp < 0)
        x.left = put(x.left, key, value);
    else
        x.right = put(x.right, key, value);

    if (isRed(x.right) && !isRed(x.left))
        x = rotateLeft(x);
    if (isRed(x.left) && isRed(x.left.left))
        x = rotateRight(x);
    if (isRed(x.left) && isRed(x.right))
        flipColors(x);

    recalculateSize(x);
    return x;
}

可以看到该插入操作和二叉查找树的插入操作类似，只是在最后加入了旋转和颜色变换操作即可。

根节点一定为黑色，因为根节点没有上层节点，也就没有上层节点的左链接指向根节点。flipColors() 有可能会使得根节点的颜色变为红色，每当根节点由红色变成黑色时树的黑链接高度加 1.

3.3.4 分析

一颗大小为 N 的红黑树的高度不会超过 2logN。最坏的情况下是它所对应的 2-3 树，构成最左边的路径节点全部都是 3- 节点而其余都是 2- 节点。

红黑树大多数的操作所需要的时间都是对数级别的。