2-2-归并排序.md

2.2 归并排序

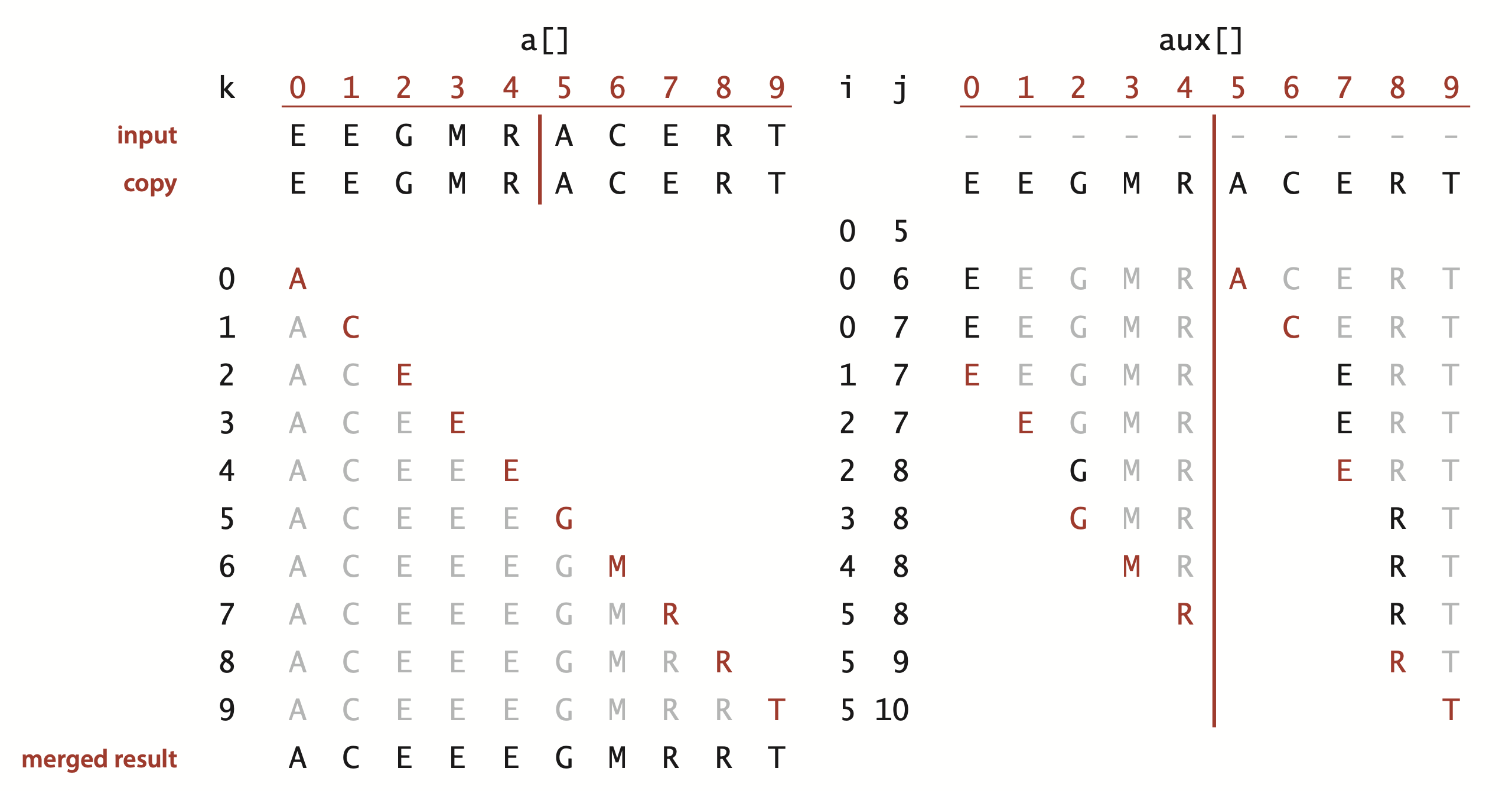
归并：将两个有序的数组归并成一个更大的有序数组。

归并排序能保证将任意长度为 N 的数组排序所需时间和 NlogN 成正比；但主要缺点是所需的额外空间和 N 成正比。

2.2.1 原地归并的抽象方法

private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
    // 先决条件: a[lo .. mid] 和 a[mid+1 .. hi] 是有序子数组
    assert isSorted(a, lo, mid);
    assert isSorted(a, mid+1, hi);

    // 拷贝到辅助数组 aux[] 中
    for (int k = lo; k <= hi; k++) {
        aux[k] = a[k]; 
    }

    // 归并到原数组 a[] 中
    int i = lo, j = mid+1;
    for (int k = lo; k <= hi; k++) {
        if      (i > mid)              a[k] = aux[j++];
        else if (j > hi)               a[k] = aux[i++];
        else if (less(aux[j], aux[i])) a[k] = aux[j++];
        else                           a[k] = aux[i++];
    }

    assert isSorted(a, lo, hi);
}

实现归并最直接的办法就是将两个有序数组归并到第三个数组中。

合并算法中 merge(a，lo，mid，hi) 将子数组的一个 [lo..mid] 与 [mid + 1..hi] 合并为一个有序数组，结果为一个 [lo..hi]。 虽然我们希望不使用大量额外空间的情况下，但是这种解决方案非常复杂。 而是，merge() 将所有内容复制到辅助数组，然后合并回原始数据。

2.2.2 自顶而下的归并排序（递归）

public class Merge {
    private static Comparable[] aux;    // 归并所需的辅助数组
    
    public static void sort(Comparable[] a) {
        aux = new Comparable[a.length];
        sort(a, 0, a.length - 1);
    }
    
    private static void sort(Comparable[] a, int lo, int hi) {
        // 将数组 a[lo..hi] 排序
        if(hi <= lo)
            return;
        int mid = lo + (hi - lo) / 2;
        sort(a, lo, mid);    // 将左半边排序
        sort(a, mid + 1, hi);    // 将右半边排序
        if(less(a[mid+1], a[mid]))    // 为 false 则认为数组已经是有序的，跳过 merge()
            merge(a, lo, mid, hi);    // 归并结果
    }
    
    public static void merge(Comparable[] a, int lo, int mid, int hi) {
        // 将 a[lo..mid] 和 a[mid+1..hi] 归并
        int i = lo, j = mid + 1;
        
        for(int k = lo; k <= hi; k++)    // 将 a[lo..hi] 复制到 aux[lo..hi]
            aux[k] = a[k];
        
        for(int k = lo; k <= hi; k++)
            if(i > mid)    // 左半边元素用尽
                a[k] = aux[j++];
            else if(j > hi)    // 右半边元素用尽
                a[k] = aux[i++];
            else if(less(aux[i], aux[j]))
                a[k] = aux[i++];
            else
                a[k] = aux[j++];               
    }
    
    private static boolean less(Comparable v, Comparable w) {
        // 对元素进行比较
        return v.compareTo(w) < 0;
    }

    private static void exch(Comparable[] a, int i, int j) {
        // 将元素交换位置
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

    private static void show(Comparable[] a) {
        // 在单行中打印数组
        for(int i = 0; i < a.length; i++)
            StdOut.print(a[i] + " ");
        StdOut.println();
    }

    public static boolean isSorted(Comparable[] a) {
        // 测试数组元素是否有序
        for(int i = 1; i < a.length; i++)
            if(less(a[i], a[i - 1]))
                return false;
        return true;
    }
}

以上代码是基础原地归并算法实现了另一种递归归并。这段递归代码是归纳证明算法能够正确将数组排序的基础：如果它能将两个字数组排序，它就能够通过归并两个子数组来将整个数组排序。

归并算法是算法设计中分治思想的典型应用。

比较次数：对于长度为 N 的任意数组，自顶向下的归并排序需要 1/2NlgN 至 NlgN 次比较。

注：N = 2 ^ n ==> n = lgN

访问数组次数：对于长度为 N 的任意数组，自顶向下的归并排序最多需要访问数组 6NlgN 次。

2.2.3 自底向上的归并排序（非递归）

public class MergeBU {

    // This class should not be instantiated.
    private MergeBU() { }

    // stably merge a[lo..mid] with a[mid+1..hi] using aux[lo..hi]
    private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {

        // copy to aux[]
        for (int k = lo; k <= hi; k++) {
            aux[k] = a[k]; 
        }

        // merge back to a[]
        int i = lo, j = mid+1;
        for (int k = lo; k <= hi; k++) {
            if      (i > mid)              a[k] = aux[j++];  // this copying is unneccessary
            else if (j > hi)               a[k] = aux[i++];
            else if (less(aux[j], aux[i])) a[k] = aux[j++];
            else                           a[k] = aux[i++];
        }

    }

    /**
     * Rearranges the array in ascending order, using the natural order.
     * @param a the array to be sorted
     */
    public static void sort(Comparable[] a) {
        int n = a.length;
        Comparable[] aux = new Comparable[n];
        for (int len = 1; len < n; len *= 2) {
            for (int lo = 0; lo < n-len; lo += len+len) {
                int mid  = lo+len-1;
                int hi = Math.min(lo+len+len-1, n-1);
                merge(a, aux, lo, mid, hi);
            }
        }
        assert isSorted(a);
    }

  /***********************************************************************
    *  Helper sorting functions.
    ***************************************************************************/
    
    // is v < w ?
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }


   /***************************************************************************
    *  Check if array is sorted - useful for debugging.
    ***************************************************************************/
    private static boolean isSorted(Comparable[] a) {
        for (int i = 1; i < a.length; i++)
            if (less(a[i], a[i-1])) return false;
        return true;
    }

    // print array to standard output
    private static void show(Comparable[] a) {
        for (int i = 0; i < a.length; i++) {
            StdOut.println(a[i]);
        }
    }

    /**
     * Reads in a sequence of strings from standard input; bottom-up
     * mergesorts them; and prints them to standard output in ascending order. 
     *
     * @param args the command-line arguments
     */
    public static void main(String[] args) {
        String[] a = StdIn.readAllStrings();
        MergeBU.sort(a);
        show(a);
    }
}