2-1-初级排序算法.md

title	tags
2019-01-27-algorithms4-first	算法 读书

2.1 排序算法类模版

public class Example {
    public static void sort(Comparable[] a) {
        // 各类排序算法
    }

    private static boolean less(Comparable v, Comparable w) {
        // 对元素进行比较
        return v.compareTo(w) < 0;
    }

    private static void exch(Comparable[] a, int i, int j) {
        // 将元素交换位置
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

    private static void show(Comparable[] a) {
        // 在单行中打印数组
        for(int i = 0; i < a.length; i++)
            StdOut.print(a[i] + " ");
        StdOut.println();
    }

    public static boolean isSorted(Comparable[] a) {
        // 测试数组元素是否有序
        for(int i = 1; i < a.length; i++)
            if(less(a[i], a[i - 1]))
                return false;
        return true;
    }

    public static void main(String[] args) {
        // 从标准输入读取字符串，将它们排序并输出
        String[] a = In.readStrings();
        sort(a);
        assert isSorted(a);
        show(a);
    }
}

• sort - 排序算法的具体实现
• less - 比较元素
• exch - 元素交换位置
• show - 打印数组
• isSorted - 判断数组元素是否有序
• main - 标准输入读取字符串，将它们排序并输出

2.1.2 选择排序(Selection sort)

public static void sort(Comparable[] a) {
    // 将 a[] 按升序排列
    int N = a.length;
    for(int i = 0 ; i < N; i++) {
        // 将 a[i] 和 a[i...N]中最小的元素交换
        int min = i;    // 最小元素的索引
        for(int j = i+1; j < N; j++)
            if(less(a[j], a[min]))
                min = j;
        exch(a, i, min);
    }
}

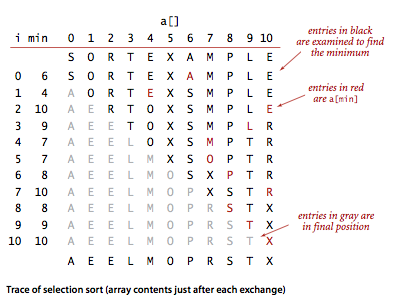
选择排序对于长度为 N 的数组，需要大约 N^2/2 次比较和 N 次交换。

选择排序的特点：

• 运行时间和输入无关：一个已经有序的数组或是主键全部相等的数组和一个元素随机排列的数组所用的排序时间一样长；
• 数据移动是最少的：每次交换都会改变两个数组元素的值，因此选择排序用了 N 次交换——交换次数和数组的大小是线性关系。其他算法大多都是线性对数或是平方级别。

2.1.3 插入排序(Insertion sort)

public static void sort(Comparable[] a) {
    // 将 a[] 按升序排列
    int N = a.length;
    for(int i = 1; i < N; i++) {
        // 将 a[i] 插入到 a[i-1]、a[i-2]、a[i-3]...之中   
        /** 有改进空间，见练习 2.1.25  */
        for(int j = i; j > 0 && less(a[j], a[j-1]); j--)
            exch(a, j, j-1);
    }
}

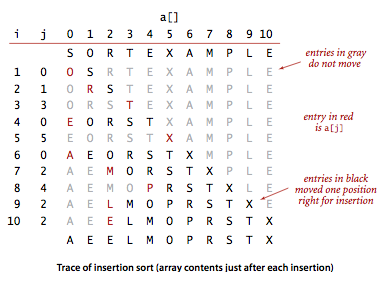
插入排序每次将正在遍历的元素插入到其他已经有序的元素中的适当位置。与选择排序一样，当前索引左边的所有元素都是有序的，但它们的最终位置还不确定。为了给更小的元素腾出空间，它们可能会向右移动。当索引到达数组的右端时，数组排序就完成了。

对于随机排列的长度为 N 且主键不重复的数组，平均情况下插入排序需要 ~N^2/4 次比较以及 ~N^2/4 次交换。最坏情况下需要 ~N^2/2 次比较和 ~N^2/2 次交换，最好情况下需要 N-1 次比较和 0 次交换。

2.1.4 排序算法可视化

2.1.5 希尔排序(Shellsort)

public static void sort(Comparable[] a) {
    // 将 a[] 按升序排列
    int N = a.length;
    int h = 1;
    while(h < N / 3)
        h = 3 * h + 1;    // 1, 4, 13, 40, 121, 364, 1093, ...
    while(h >= 1) {
        // 将数组变为 h 有序
        for(int i = h; i < N; i++) {
            // 将 a[i] 插入到 a[i-h]，a[i-2*h]，a[i-3*h]... 之中
            for(int j = i; j >= h && less(a[j], a[j -h]); j -= h)
                exch(a, j, j-h);
        }
        h /= 3;
    }
}

希尔排序是一种基于插入排序的快速的排序算法，为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。

思想：使数组中任意间隔为 h 的元素都是有序的。这样的数组被称为 h 有序数组。换句话说，一个 h 有序数组就是 h 个互相独立的有序数组编织在一起的一个数组。